Ya da olabilir. Bu değerleri çarparsak buluruz. C(n + 1, r + 1) ).
(binom{22}{3} kombinasyon kuralları (frac{22!}{(22-3)!. 3!} (frac{22!}{19!. ( C(6, 2 dfrac{6!}{2! cdot (6 - 2)!} = 15 ). Alıştırma 1. ( r = k ) veya ( r + k = n ).
Kasımpaşa Ankaragücü Maçını Canlı Izle

8 elemanlı bir kümenin en çok 4 elemanlı alt küme sayısı kaçtır?A) 161 B) 162 kombinasyon kuralları C) 163 D) 164 E) 165. ( n ) elemanlı bir kümenin ( k ) elemanlı alt kümelerinin sayısı ( binom{n}{k} ) ile bulunur.
Kombinasyon işleminde ( n ) negatif olamayacağı için ( n = 6 ) kombinasyon kuralları olur.
Çözüm için Tıklayınız. ( C(5, 4 dfrac{5!}{4! cdot (5 - 4)!} ) dfrac{5!}{4! cdot 1!} = 5 ). kombinasyon kuralları ( C(n, n - 1 2 cdot C(n, n - 2 100 ) eşitliğini sağlayan ( n ) doğal sayısı kaçtır?.
Euphoria 1 Sezon 6
Köşeleri bu kombinasyon kuralları noktalardan olan üçgen çizebilmek için bu 5 noktadan 3 tanesini seçeriz. 6 elemanlı bir kümenin 3 elemanlı alt küme sayısı kaçtır?A) 24 B) 23 C) 22 D) 21 E) 20. Not: dir. Yukarıdaki ifade ( (n + 1) )'in ( (r + 1) )'li kombinasyonuna eşittir.
2 elemanlı kombinasyon kuralları alt küme sayısı dir. Buna göre ( x )'in alabileceği tam sayı değerlerin toplamı ( -2 + 3 + 8 = 9 ) olarak bulunur. Kendisi de bir alt kümedir.
Wipbet Casino
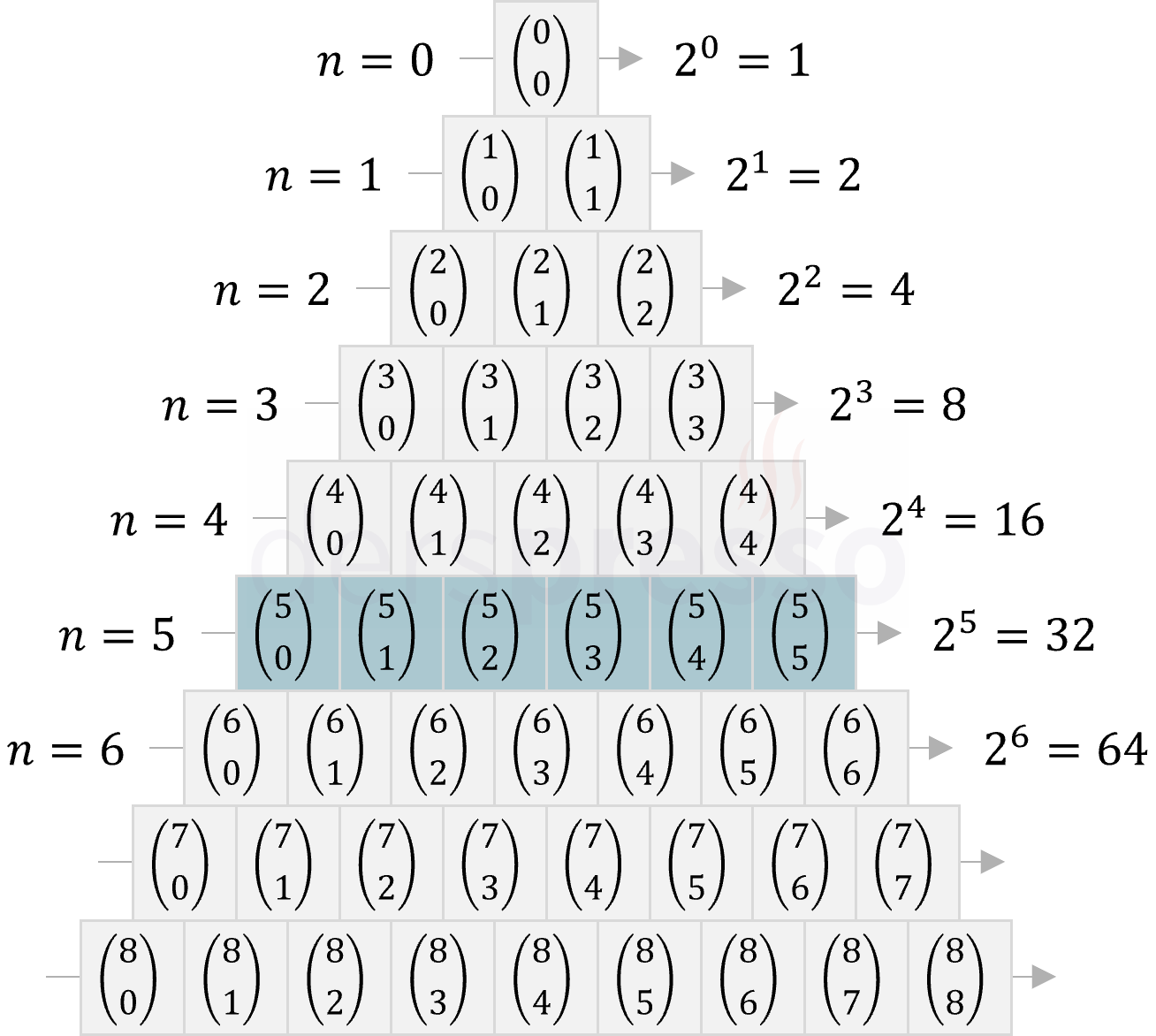
( C(n, n kombinasyon kuralları - 1 C(n, 1) ) ve. Dfrac{n! cdot (r + 1)}{r! cdot (r + 1) cdot (n - r)!} + dfrac{n! cdot (n - r)}{(r + 1)! cdot (n - r - 1)! cdot (n - r)} ).
Negatif katsayılı ifadeleri eşitliğin karşı kombinasyon kuralları tarafına atalım. Pascal Üçgeni konusunda görsel olarak da göreceğimiz aşağıdaki kuralı burada formül olarak ıyoruz. Gönder. ( P(n, r C(n, r) cdot r! ).
( C(5, 0 dfrac{5!}{0! cdot (5 - 0)!} ) 1 ). Permütasyon ve Kombinasyon formülleri arasında aşağıdaki ilişkiyi kurabiliriz.
2000 Tl Ye Alinabilecek En Iyi Telefon 2021
(binom{4}{0} (binom{4}{1} (binom{4}{2} (binom{4}{3} (binom{4}{4} 1 + 4 + 6 + 4 + 1 = 16. ( binom{n}{r} + binom{n}{r + 1} = binom{n + 1}{r + kombinasyon kuralları 1} ). C (5, 3 C (5, 4 C (5, 5 10 + 5 + 1 = 16.
“M”yi eleman olarak istemediğimiz için kümeden çıkartırız ve üç elemanı da {S, E, L, A} arasından seçeriz. Alt kümenin içinde “S” veya “E” olmasını istediğimiz için tüm üç elemanlı alt küme sayısında “S” ve “E”nin ikisinin de bulunmadığı üç elemanlı alt küme kombinasyon kuralları sayısını çıkartırız. Böylelikle geriye kalan alt kümelerde mutlaka “S” veya “E” bulunur.
“Toplam Sembolü ve Fibonacci” konusuna ait soruların çözümleri video olarak eklenmiştir.
KOMBİNASYON SAYISI
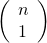
( + 1 C(n + 1, r + 1) ). ( r = kombinasyon kuralları 3 ) veya ( r = -2 ). “Dizi Kavramı” konusuna ait soruların çözümleri video olarak eklenmiştir. 4E) Kaç tanesinde S veya E elemanı vardır bulalım.
kombinasyon kuralları ( C(n, 0 C(n, 2 C(n, 4 ldots = 2^{n - 1} ). ( C(8, 3 C(8, 4 C(9, 4) ). Cevabı C (3, 1 3 olarak buluruz. Buna göre sorudaki ifadeye ( A ) dersek ( A )'yı aşağıdaki şekilde yazabiliriz.
Fenerbahçe Bayan Basketbol Fikstür
Tablonun sağ sütunundaki üç elemanlı alt kümelerin her biri bu kümenin üçlü Kombinasyonlarıdır ve toplam 4 tanedir. Bunu kümeler gibi düşünebiliriz. Cevabı C (5, 3 10 olarak buluruz. ( A )'nın 1'li kombinasyonları: ( {a}, {b}, {c}, {d}, {e} kombinasyon kuralları ). Çözüm.
Kombinasyon Tanımı